モーメントとキュムラントの関係

統計学

モーメントとキュムラントはそれぞれ一方だけで表すことができる. その導出を行った.

モーメント母関数からモーメントの導出

モーメントはモーメント母関数から導出できる. 確率変数 Xの r次のモーメントを \mu'_r(=E[X^r]), モーメント母関数を M_X(t)とおくと

{\displaystyle \begin{align} M_X(t)&=E[\exp(tX)]\\ &=\int^{\infty}_{-\infty}\exp(tx)p(x)dx\\ &=\int^{\infty}_{-\infty}\{\sum^{\infty}_{r=0}{\frac{1}{r!}(xt)^r}\}p(x)dx\\ &=\sum^{\infty}_{r=0}\frac{\int^{\infty}_{-\infty}x^rp(x)dx}{r!}t^r\\ &=\sum^{\infty}_{r=0}\frac{E[X^r]}{r!}t^r\\ &=\sum^{\infty}_{r=0}\frac{\mu'_r}{r!}t^r \end{align}}

よって

{\displaystyle \begin{align} \mu'_r=\frac{\partial^r M_X(t)}{\partial t^r}|_{t=0} \end{align}}

キュムラント母関数とキュムラント

キュムラント母関数 K_X(t)は以下で定義される.

{\displaystyle \begin{align} K_X(t)=log(M_X(t)) \end{align}}

よって

{\displaystyle \begin{align} K_X(t)=log(\sum^{\infty}_{r=0}\frac{E[X^r]}{r!}t^r) \end{align}}

と書くことができ,

{\displaystyle \begin{align} \kappa_r=\frac{\partial^r K_X(t)}{\partial t^r}|_{t=0} \end{align}}

とすれば

{\displaystyle \begin{align} K_X(t)=\sum^{\infty}_{r=0}\frac{\kappa_r}{r!}t^r \end{align}}

と書くことができる. \kappa_rを r次のキュムラントという.

モーメントとキュムラントの関係式

モーメント母関数とキュムラント母関数の関係は

{\displaystyle \begin{align} M_X(t)&=\exp(K_X(t))\\ \Leftrightarrow \sum^{\infty}_{r=0}\frac{\mu'_r}{r!}t^r &= \exp(\sum^{\infty}_{r=0}\frac{\kappa_r}{r!}t^r) \end{align}}

であるので, 両辺を \kappa_jで偏微分すると

{\displaystyle \begin{align} \sum^{\infty}_{r=0}\frac{1}{r!}\frac{\partial \mu'_r}{\partial \kappa_j}t^r &= \frac{1}{j!}t^j\exp(\sum^{\infty}_{r=0}\frac{\kappa_r}{r!}t^r)\\ &=\frac{1}{j!}t^j \sum^{\infty}_{r=0}\frac{\mu'_r}{r!}t^r\\ &=\sum^{\infty}_{r=0}\frac{\mu'_r}{j!r!}t^{j+r}\\ &=\sum^{\infty}_{r=j}\frac{\mu'_{r-j}}{j!(r-j)!}t^r \quad (j+r\rightarrow r) \end{align}}

両辺で t^rの係数を比較すれば以下の関係が得られる.

{\displaystyle \begin{align} \frac{\partial \mu'_r}{\partial \kappa_j} = \begin{cases} 0 \quad\quad\quad\quad (r < j)\\ \begin{pmatrix} r \\ j \end{pmatrix} \mu_{r-j} \quad (r\geqq j)\\ \end{cases} \end{align}}

特に j=1のとき

{\displaystyle \begin{align} \frac{\partial \mu'_r}{\partial \kappa_1} = r\mu'_{r-1} \end{align}}

モーメントとキュムラントの関係式（具体的に）

まず, モーメント母関数とキュムラント母関数の関係から

{\displaystyle \begin{align} M_X(t)&=\exp(K_X(t))\\ \Leftrightarrow \sum^{\infty}_{r=0}\frac{\mu'_r}{r!}t^r &= \exp(\sum^{\infty}_{r=0}\frac{\kappa_r}{r!}t^r)\\ &=\prod^{\infty}_{r=0}\exp(\frac{\kappa_r}{r!}t^r)\\ &=\prod^{\infty}_{r=0}\sum^{\infty}_{s=0}\frac{(\frac{\kappa_r}{r!}t^r)^s}{s!} \end{align}}

ここから, t^rの係数を比較して \mu'_rを得るが, 式から \mu'_rは \kappa_j \ (j=1,2,\dots)のみで構成されていることが分かる.

\mu'_1を求める

r=1のとき

{\displaystyle \begin{align} \frac{\partial \mu'_1}{\partial \kappa_1} &= 1\cdot \mu'_0\\ &=1\cdot \int^{\infty}_{-\infty}p(x)dx=1\\ \Leftrightarrow \mu'_1&=\int 1 d\kappa_1\\ &=\kappa_1+C(\kappa\backslash\kappa_1)\\ \end{align}}

ただし, C(\kappa\backslash\kappa_1)は \kappa_1以外の \kappa_j (j=1,2,\dots)の関数を意味する.
さらに, \frac{\partial \mu'_1}{\partial \kappa_j}=0 (j > 1)であり, \mu'_rは \kappa_j (j=1,2,\dots)のみで構成されていることから C(\kappa\backslash\kappa_1)=0である.
以上より

{\displaystyle \begin{align} \mu'_1=\kappa_1 \end{align}}
\mu'_2を求める
{\displaystyle \begin{align} \frac{\partial \mu'_2}{\partial \kappa_1} &= 2\mu'_1\\ &=2\kappa_1\\ \Leftrightarrow \mu'_2&=\int 2\kappa_1d\kappa_1\\ &=\kappa^2_1+C(\kappa\backslash\kappa_1) \end{align}}

これより,

{\displaystyle \begin{align} \frac{\partial \mu'_2}{\partial \kappa_2} = \frac{\partial}{\partial \kappa_2}(\kappa^2_1+C(\kappa\backslash\kappa_1)) = 0 + \frac{\partial C(\kappa\backslash\kappa_1)}{\partial \kappa_2} \end{align}}

また, モーメントとキュムラントの関係式より

{\displaystyle \begin{align} \frac{\partial \mu'_2}{\partial \kappa_2} = \begin{pmatrix} 2 \\ 2 \end{pmatrix} \mu'_0 =1 \end{align}}

これらより

{\displaystyle \begin{align} C(\kappa\backslash\kappa_1)=\kappa_2+C(\kappa\backslash\kappa_1\kappa_2) \end{align}}

\frac{\partial \mu'_2}{\partial \kappa_j}=0 \ (j > 2)であり, \mu'_rは \kappa_j \ (j=1,2,\dots)のみで構成されていることから C(\kappa\backslash\kappa_1\kappa_2)=0. 以上より

{\displaystyle \begin{align} \mu'_2=\kappa_2+\kappa^2_1 \end{align}}
\mu'_3を求める
{\displaystyle \begin{align} \frac{\partial \mu'_3}{\partial \kappa_1} &= 3\mu'_2\\ &=3\kappa_2+3\kappa^2_1\\ \Leftrightarrow \mu'_3&=\int (3\kappa_2+3\kappa^2_1)d\kappa_1\\ &=3\kappa_1\kappa_2+\kappa^3_1+C(\kappa\backslash\kappa_1) \end{align}}

これより,

{\displaystyle \begin{align} \frac{\partial \mu'_3}{\partial \kappa_2} = \frac{\partial}{\partial \kappa_2}(3\kappa_1\kappa_2+\kappa^3_1+C(\kappa\backslash\kappa_1)) = 3\kappa_1 + 0 + \frac{\partial C(\kappa\backslash\kappa_1)}{\partial \kappa_2} \end{align}}
{\displaystyle \begin{align} \frac{\partial \mu'_3}{\partial \kappa_3} = \frac{\partial}{\partial \kappa_3}(3\kappa_1\kappa_2+\kappa^3_1+C(\kappa\backslash\kappa_1)) = 0 + 0 + \frac{\partial C(\kappa\backslash\kappa_1)}{\partial \kappa_3} \end{align}}

また, モーメントとキュムラントの関係式より

{\displaystyle \begin{align} \frac{\partial \mu'_3}{\partial \kappa_2} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} \mu'_1 =3\kappa_1 \end{align}}
{\displaystyle \begin{align} \frac{\partial \mu'_3}{\partial \kappa_3} = \begin{pmatrix} 3 \\ 3 \end{pmatrix} \mu'_0 =1 \end{align}}

これらより

{\displaystyle \begin{align} \begin{cases} C(\kappa\backslash\kappa_1)=const+C(\kappa\backslash\kappa_1\kappa_2)\\ C(\kappa\backslash\kappa_1)=\kappa_3+C(\kappa\backslash\kappa_1\kappa_3)\\ \end{cases}\\ \Leftrightarrow C(\kappa\backslash\kappa_1) = \kappa_3 + const + C(\kappa\backslash\kappa_1\kappa_2\kappa_3) \end{align}}

\frac{\partial \mu'_3}{\partial \kappa_j}=0 \ (j > 3)であり, \mu'_rは \kappa_j \ (j=1,2,\dots)のみで構成されていることから C(\kappa\backslash\kappa_1\kappa_2\kappa_3). 以上より

{\displaystyle \begin{align} \mu'_3=\kappa_3+3\kappa_1\kappa_2+\kappa^3_1 \end{align}}

 

\mu'_4以降も同様にすれば導出できる.

参考

Kendall, Maurice, and Alan Stuart. "The advanced theory of statistics. Vol. 1: Distribution theory." London: Griffin, 1977, 4th ed. (1977).

WindowsからUbuntuにリモートデスクトップ

Windows Linux

Windows機からUbuntu機をリモートデスクトップで操作する方法（LANのみ）。

手順

Ubuntu機をvncで操作できるようにする

  • 下記コマンドでUbuntu機にx11vncをインストールします。
$ sudo apt-get install x11vnc
  • 下記コマンドでx11vncのパスワードを設定します。
$ x11vnc -storepasswd
  • 下記コマンドでx11vncを起動します。起動後文がずらずらと出てくるのでポート番号「PORT=xxxx(デフォルトでは5900)」の部分を覚えておいてください。また、後でvncで接続するので起動したままにしておいでください。
x11vnc -usepw

-usepwをつけるとvncを利用するときに先程設定したパスワードが要求されます。

  • Windows機にUltraVNC Viewerをインストールします。

  • UltraVNC Viewerを開くと一番上に「VNC Server:」という入力欄があるのでここにUbuntu機のipアドレス+:ポート番号を入力して「Connect」を押します。
    ex. ipアドレスが192.168.3.11, ポート番号が5900の場合は192.168.3.11:5900と入力

  • パスワード要求画面が出てくるのでx11vncで設定したパスワードを入力します。Ubuntu機の画面が出てきたら成功です。

※ 「Failed to connect to server !」と出る場合はUbuntu機でx11vncが起動されているか確かめてください。

ssh経由でvncを利用する

単純にvncでwindows機からUbuntu機をGUIで操作するだけなら上記までで問題ありません。しかし、vnc接続は暗号化がされていないので安全な接続とは言えません。そのため、sshを経由し、暗号化することで安全なvnc接続をします。

Ubuntu機をsshで操作できるようにする

  • 下記コマンドでUbuntu機にopenssh-serverをインストールします。
$ sudo apt-get install openssh-server
$ ifconfig

inetアドレス:xxx.xxx.xxx.xxxの部分がipアドレスです。

  • Windows機にTera Tremをインストールします。

  • Tera Tremを開くと「新しい接続」画面が出るので、「TCP/IP」を選択し、「ホスト（Ｔ）」にubuntu機のipアドレスを入力して「ＯＫ」を押します。

  • 「SSH認証」という画面が出てくるので「ユーザー名（Ｎ）」と「パスフレーズ（Ｐ）」にubuntu機のアカウントのユーザー名とパスワードを入力して「ＯＫ」を押します。

  • 端末のような黒い画面が出てきたらsshでの接続成功です。CUIでUbuntu機を操作することができます。

  • 接続ができることを確認したら一度Tera Termを閉じます。

sshポートフォワーディングによりvnc接続を行う

sshポートフォワーディングとはsshの経路を使用して他の通信を行うことです。
ここではUbuntu機のvncの通信をsshの経路を経由してWindows機のlocalhostのポートに転送します。
そして、localhostのポートをUltraVNC Viewerで接続します。

  • Tera Termを開きます。「新しい接続」画面は閉じて、「設定」→「SSH転送」を開きます。

  • 「SSHポート転送」画面が出てくるので「ローカルのポート」を選択し、
    「ローカルのポート」にはlocathostのポート番号（0～65535の任意のポート番号を設定）
    「リッスン」は空欄
    「リモート側のホスト」にはUbuntu機のipアドレス
    「ポート」にはx11vncのポート番号
    を入力し、「ＯＫ」を押して「SSHポート転送」画面を閉じます。

  • 「設定」→「設定の保存」で設定を保存します。保存名を「TERATERM.INI」にすると毎回この設定が読み込まれます。

  • 「ファイル」→「新しい接続」で「新しい接続」画面が出るのでUbuntu機にssh接続してください。

  • ssh接続した画面で「x11vnc -usepw」とコマンドし、Ubuntu機でx11vncを起動させます。

  • Windows機でUltraVNC Viewerを起動し、「VNC Server:」にlocathost::+locathostのポート番号を入力し「Connect」を押します。
    ex. locathostのポート番号を12345としたときlocathost::12345と入力する。

  • x11vncで設定したパスワードを入力し、Ubuntu機のGUI画面が出てきたら成功です。

カオス時系列解析 -観測時系列からのアトラクタ再構成-

カオス時系列解析 時系列解析

はじめに

力学系のアトラクタを得ることはカオス時系列解析を行うためには非常に重要です.
しかし現実問題として力学系の時系列 {\boldsymbol{x}(t)}そのものが得られることはまれで, 大抵は力学系を観測することによって得られた1次元の観測時系列 \{y_n\}しか得られません.

{\boldsymbol{x}(t)}と {y_n}の関係は以下のようにして数式で表されます.

{\begin{align} y_n = g(\boldsymbol{x}(n\Delta t)) + \eta_n \end{align}}

だたし, 関数 gは観測操作に相当する関数, \Delta tはサンプリング間隔, \eta_nは観測ノイズ.
我々が得ている時系列は大抵 {y_n}と同様のプロセスを踏んでいます. {y_n}から元の力学系のアトラクタを再構成するためにはどうすれば良いのでしょうか？

この話をローレンツ方程式を例にして具体的に考えてみます. ローレンツ方程式は以下で表される力学系です.

{\displaystyle \begin{align} \frac{dx}{dt}&=-px+py\\ \frac{dy}{dt}&=-xz+rx-y\\ \frac{dz}{dt}&=xy-bz \end{align}}

ローレンツ方程式は3次元の力学系で下のような軌跡を描きます（アトラクタ）.

f:id:richard392742:20180923200155p:plain
ローレンツ方程式の状態変数の軌跡（アトラクタ）

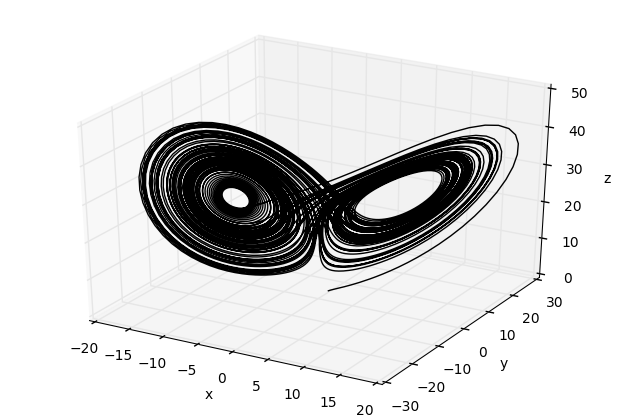
実際に時系列解析が行われるときは, この力学系 x,y,z全ての時系列が得られることはまれで, 観測により xのみの時系列が得られるようなケースが多いです（つまり観測時系列は g(\boldsymbol{x})=x, \eta_n=0で得られた）.

f:id:richard392742:20181008025736p:plain
ローレンツ方程式のxの時系列

このようなとき, xの時系列のみで元の3次元の力学系の構造や振る舞いを把握することは可能でしょうか？

時間遅れ座標系とTakensの埋め込み定理

アトラクタの再構成のために良く使用されるのが「時間遅れ座標系」と呼ばれる座標系への変換です. この変換では観測時系列 \{y_n\}は以下の様に m次元ベクトルの時系列 \{\boldsymbol{v}_n\}変換されます.

{\displaystyle \begin{align} \boldsymbol{v}_n = (y_n,y_{n-\tau},\dots,y_{n-(m-1)\tau}) \end{align}}

ただし, \tauは時間遅れの大きさ. また \boldsymbol{v}の次元数 mは埋め込み次元と呼ばれます.

このようにして構成された遅れ座標系は本当に元の力学系のアトラクタを再構成できるのでしょうか？また, 再構成ができるのであれば mはいくつにすればいいのでしょうか？ これらの問題は「Takensの埋め込み定理」により保証されています.

Takensの埋め込み定理
d次元のコンパクトな多様体 Dと C^1級写像 \boldsymbol{f}:D\to D, g:D\to \mathbb{R}^1が与えられたとき, m>2dであれば, 次式の写像 V:D\to \mathbb{R}^mは埋め込みである.
{\begin{align} V(\boldsymbol{x})=(g(\boldsymbol{x}),g(\boldsymbol{f}(\boldsymbol{x})),g(\boldsymbol{f}^2(\boldsymbol{x})),\dots,g(\boldsymbol{f}^{m-1}(\boldsymbol{x}))) \end{align}}

「埋め込み」について

「埋め込みである」とはどういう意味でしょうか？
ある多様体 Dに対し, 写像 Vが埋め込みであるとは, 写像 Vが以下を満たすということです.

  1. Vが1対1写像である
  2. Vの微分が1対1写像である
  3. Dに対し, Vが同相写像(位相空間 A,Bの間の写像 f:A→Bが連続かつ全単射で, その逆写像もまた連続である写像のこと)である

1.と2.の性質について下図の例で見てみます.

f:id:richard392742:20181006023011p:plain

この図では多様体 Mが写像 Vにより写されたときを3つのパターンで示しています.

Vが埋め込みのときは一番右のようになります.
Vが2.の性質を満たしていない場合は真ん中のように微分が不可能な部分ができます.
Vが1.の性質を満たしていない場合は左のように重なって1対1とならない部分ができます.

このように \boldsymbol{x}の軌道が再構成されるためには図の真ん中や右のようにはならず, かつ同相である写像でなければなりません.
Takensの埋め込み定理の「埋め込みである写像」とは「元の力学系の構造や振る舞いを保存する写像」と解釈できます.

写像 Vについて

Takensの埋め込み定理の写像 Vは「力学系を観測し, 観測時系列を遅れ座標系にする」という操作に対応しています.
V内の関数 \boldsymbol{f}を力学系の状態変数 \boldsymbol{x}を一時刻先へ時間発展をさせる関数 \boldsymbol{f}:\boldsymbol{x}_t \to \boldsymbol{x}_{t+1}と考えます. そうすれば

{\begin{align} \boldsymbol{x}_t,\boldsymbol{f}(\boldsymbol{x}_t),\boldsymbol{f}^2(\boldsymbol{x}_t),\dots,\boldsymbol{f}^{m-1}(\boldsymbol{x}_t)=\boldsymbol{x}_t,\boldsymbol{x}_{t+1},\dots,\boldsymbol{x}_{t+m-1} \end{align}}
となります.
これに観測関数 \boldsymbol{g}をかけると観測時系列になり, さらに, これは写像 Vでもあります.

{\begin{align} (y_t,y_{t+1},\dots,y_{t+(m-1)}) &=\boldsymbol{g}(\boldsymbol{x}_t,\boldsymbol{x}_{t+1},\dots,\boldsymbol{x}_{t+m-1})\\ &=(g(\boldsymbol{x}_t),g(\boldsymbol{f}(\boldsymbol{x}_t)),g(\boldsymbol{f}^2(\boldsymbol{x}_t)),\dots,g(\boldsymbol{f}^{m-1}(\boldsymbol{x}_t)))\\ &=V(\boldsymbol{x}_t) \end{align}}

今回 \boldsymbol{f}は時間発展の関数としていましたが, 逆に時間を遅れさせる関数 \boldsymbol{f}:\boldsymbol{x}_{t+1} \to \boldsymbol{x}_tとしても良く, そうすると上の観測時系列は遅れ座標系になります.
また, 一時刻を \tauとすれば (y_n,y_{n-1},\dots,y_{n-(m-1)}) \to (y_n,y_{n-\tau},\dots,y_{n-(m-1)\tau})ではじめの遅れ座標系と同じになります.

Takensの埋め込み定理が言いたいこと

Takensの埋め込み定理は遅れ座標系を導入したとき, 元の力学系の構造や振る舞いが保存されるのに十分な mの値を与えてくれています. 元の力学系の次元数 dに対し, m=2d+1以上とすれば十分であることを保証しています.
なぜ元の次元数の2倍より大きな mが必要なのでしょうか？
ここで下図のような \mathbb{R}^d上の1次元多様体 Dを様々な mでの写像 Vで写すことを考えてみます.

f:id:richard392742:20181006023042p:plain

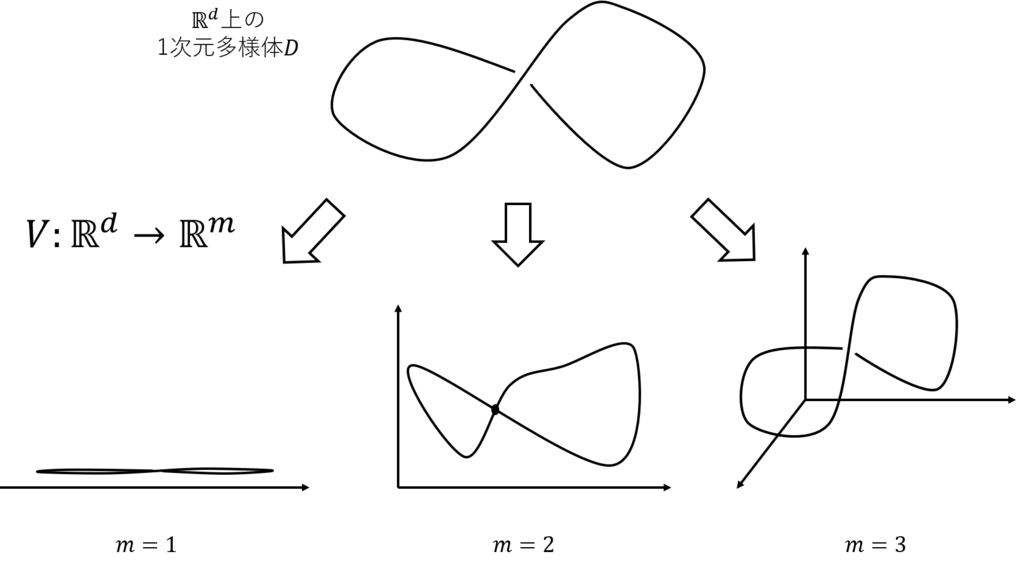
m=1のときは元の多様体上の点が重なり軌道が再構成できないことがわかります.
m=2のときも重なる部分があり, 軌道を完全には再構成できません.
m=3のときは重なるようなことはほぼありません. 例え重なるようなときでも観測関数に摂動を加える（現実ではこれは観測ノイズとして必ず入ってくる）ことで重なりは容易に解消されます.

実際にやってみる

先のローレンツ方程式で確認してみましょう.

import numpy as np
from scipy.integrate import ode
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 力学系のパラメータ設定
p = 10.0
r = 28.0
b = 8.0/3.0

# 力学系の関数を設定
def x_dot(x, y):
    return -p*x + p*y

def y_dot(x, y, z):
    return - x * z + r * x - y

def z_dot(x, y, z):
    return x * y - b * z

def lorenz(t, v):
    '''v = [x, y, z]'''
    return [x_dot(v[0],v[1]), y_dot(v[0],v[1],v[2]), z_dot(v[0],v[1],v[2])]

# 初期値の設定
t0 = 0.0
x0, y0, z0 = 1.0, 1.0, 1.0

# シミュレーションの時間間隔
dt = 0.01

# シミュレーション時間
T = 100.0

# 数値計算を行うオブジェクトの作成
integrator = ode(lorenz).set_integrator('dopri5')
integrator.set_initial_value([x0,y0,z0], t0)

# シミュレーション
time = []
data = []
for t in np.arange(t0, T, dt):
    time.append(integrator.t+dt)
    data.append(integrator.integrate(integrator.t+dt))
data = np.array(data)

# 観測によりxの時系列を得る
x = data[:, 0]

# アトラクタ再構成
def get_delay_coordinate(x, dt, m, tau):
    interval = tau/dt
    vs = [np.array([x[i-int(interval*j)] for j in range(m)])
         for i in range(int(interval*(m-1)), len(x))]
    return vs

tau = 0.1
m = 3

vs = get_delay_coordinate(x, dt, m, tau)
vs = np.array(vs)

fig = plt.figure()
ax = Axes3D(fig)
ax.plot(vs[:,0], vs[:,1], vs[:,2], lw=1, c='k')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()

f:id:richard392742:20181008055902p:plainf:id:richard392742:20181008055824p:plainf:id:richard392742:20181008055827p:plain
m=3, \tau=0.01のとき
f:id:richard392742:20181008055829p:plainf:id:richard392742:20181008055832p:plainf:id:richard392742:20181008055837p:plain
m=3, \tau=0.1のとき
f:id:richard392742:20181008055847p:plainf:id:richard392742:20181008055858p:plainf:id:richard392742:20181008055853p:plain
m=3, \tau=1.0のとき
f:id:richard392742:20181008063728p:plain:w200
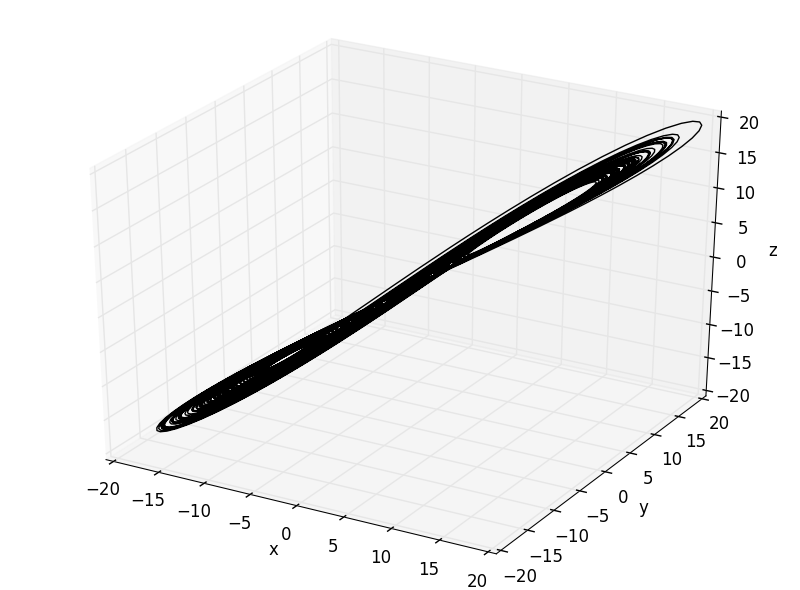
m=2, \tau=0.1のとき

この中では m=3, \tau=0.1のとき, 最も上手くいっており, 1次元の遅れ座標系の軌跡が元のアトラクタとよく似ているように見えます.
本来であればローレンツ方程式は3次元力学系なのでTakensの埋め込み定理が保証してくれるのは m=7からですが, Takensの埋め込み定理は十分条件なのでこのように実は m=3でも元のアトラクタが再構成できてしまうこともあります. mの最小値を求めるには, 「False nearest neighbors」などの手法を使用する必要があります(今までのは何だったのか).
また, Takensの埋め込み定理では \tauはほぼ任意であるのですが, 現実的にはデータの有限性やノイズなどの理由から, やはり \tauも最適なものを求める必要があります. 方法としては自己相関関数を使用して求めるようです.

参考

合原一幸(編). "カオス時系列解析の基礎と応用" 産業図書(2000). Kantz, Holger, and Thomas Schreiber. Nonlinear time series analysis. Vol. 7. Cambridge university press, 2004. Hegger, Rainer, Holger Kantz, and Thomas Schreiber. "Practical implementation of nonlinear time series methods: The TISEAN package." Chaos: An Interdisciplinary Journal of Nonlinear Science 9.2 (1999): 413-435.

カオス時系列解析 - 力学系とアトラクタ -

カオス時系列解析 時系列解析

力学系とは？

力学系とはある時刻における状態が、微分方程式、差分方程式、微差分方程式により決定されるシステムのこと。
$k$次元力学系では、任意の時刻におけるシステムの状態の変化則は$k$個の状態変数の関数により記述される。

離散時間力学系の場合： $$ x(t+1)=\boldsymbol{f}_\boldsymbol{\mu}(\boldsymbol{x}(t)) $$

連続時間力学系の場合： $$ \frac{dx(t)}{dt}=\boldsymbol{f}_\boldsymbol{\mu}(\boldsymbol{x}(t)) $$

但し、$\boldsymbol{x}(t)$は時間$t$における力学系の状態空間を構成する多様体上のシステムの状態、$\boldsymbol{f}$は$k$次元の非線形関数、$\boldsymbol{\mu}$はシステムを制御するパラメータベクトル。
先述のこれらの式のように$\boldsymbol{f}$内に明示的に時間$t$が含まれていない系を自律系（automonous system）という。これに対し、

$$ x(t+1)=\boldsymbol{f}_\boldsymbol{\mu}(\boldsymbol{x}(t),t) $$

や $$ \frac{dx(t)}{dt}=\boldsymbol{f}_\boldsymbol{\mu}(\boldsymbol{x}(t),t) $$

のように$\boldsymbol{f}$内に明示的に時間$t$が含まれている系を非自律系（non-automonous system）という。

アトラクタとは？

力学系に初期条件を与え、十分時間が経った後の$k$次元状態空間内での漸近的な振る舞いのこと。
例として以下で与えられるローレンツ方程式のアトラクタを見てみる。

ローレンツ方程式: $$ \begin{eqnarray} \frac{dx}{dt}&=&-px+py\\ \frac{dy}{dt}&=&-xz+rx-y\\ \frac{dz}{dt}&=&xy-bz \end{eqnarray} $$ 但し、$p,r,b$はそれぞれシステムを制御するパラメータで、$p=10,r=28,b=\frac{8}{3}$のとき、ローレンツ方程式はカオス的な挙動をすることが知られている。
参考：https://ja.wikipedia.org/wiki/%E3%83%AD%E3%83%BC%E3%83%AC%E3%83%B3%E3%83%84%E6%96%B9%E7%A8%8B%E5%BC%8F

import numpy as np
from scipy.integrate import ode
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 力学系のパラメータ設定
p = 10.0
r = 28.0
b = 8.0/3.0

# 力学系の関数を設定
def x_dot(x, y):
    return -p*x + p*y

def y_dot(x, y, z):
    return - x * z + r * x - y

def z_dot(x, y, z):
    return x * y - b * z

def lorenz(t, v):
    '''v = [x, y, z]'''
    return [x_dot(v[0],v[1]), y_dot(v[0],v[1],v[2]), z_dot(v[0],v[1],v[2])]

# 初期値の設定
t0 = 0.0
x0, y0, z0 = 1.0, 1.0, 1.0

# シミュレーションの時間間隔
dt = 0.01

# シミュレーション時間
T = 100.0

# 数値計算を行うインスタンスの作成
integrator = ode(lorenz).set_integrator('dopri5')
integrator.set_initial_value([x0,y0,z0], t0)

# シミュレーション
time = []
data = []
for t in np.arange(t0, T, dt):
    time.append(integrator.t+dt)
    data.append(integrator.integrate(integrator.t+dt))
data = np.array(data)

# 描画
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(data[:,0], data[:,1], data[:,2],
        lw=1, c='k')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()

f:id:richard392742:20180923200155p:plain

アトラクタの種類

アトラクタの形状は以下のように分類される。
1. 平衡点
2. リミットサイクル
3. トーラス
4. ストレンジアトラクタ、カオス

参考

合原一幸(編). "カオス時系列解析の基礎と応用" 産業図書(2000).

カオス時系列解析 - 序論 -

カオス時系列解析 時系列解析

カオス現象（決定論カオスの場合）

  • カオス現象：時系列を生成するシステムが決定的であるのにも関わらず,システム自体の非線形性によって,あたかもランダムな時系列と同じような時系列が生み出される現象.
  • このような時系列に対し,主に使用される時系列解析法である周波数解析や線形モデリング手法（AR,MAモデル）といった線形理論に基づく解析が不適切な場合が出てきた.
  • システムの非線形性によって生成された時系列の特徴を線形理論に基づく解析では「ノイズ」とみなし,無視し続けてきた可能性がある.
  • カオス時系列解析は「ノイズ」とみなされてきた部分に,システムの非線形性が寄与している可能性を考慮にいれて解析を行う.

カオス時系列の例:

まず,カオス時系列の例とランダムな時系列を見てみる.

import numpy as np
import matplotlib.pyplot as plt

# システム:ロジスティックマップ
def system1(x):
    return 4 * x * (1 - x)

t_len = 1000

# ロジスティックマップが生成する時系列
x0 = 0.2
xs = [x0]
for t in range(t_len):
    x = system1(xs[-1])
    xs.append(x)
    
# [0,1)の一様乱数
np.random.seed(111)
r_xs = np.random.uniform(0,1,t_len)

plt.subplot(2,1,1)
plt.plot(xs, lw=0.5)
plt.ylim(-0.1,1.1)
plt.subplot(2,1,2)
plt.plot(r_xs, lw=0.5)
plt.ylim(-0.1,1.1)
plt.show()

f:id:richard392742:20180918050021p:plain

上がロジスティックマップと呼ばれるシステムから生成される時系列.
下が区間[0,1)の一様乱数.
パッと見,上もランダムな時系列に見えるが,これはシステムにより決定論的（確率的ではない）に得られたものである.
このような時系列がカオス時系列である.

※ロジスティックマップは以下で表される力学系（システム）である. $$ x_{t+1} = ax_t(1-x_t) $$ $a \in [0,4]$の値によって安定不動点,周期解,カオスと振る舞いが変化する.
参考：
https://ja.wikipedia.org/wiki/%E3%83%AD%E3%82%B8%E3%82%B9%E3%83%86%E3%82%A3%E3%83%83%E3%82%AF%E5%86%99%E5%83%8F

次に両時系列のパワースペクトル密度（PSD）を求めてみる.

plt.figure(figsize=(10,4))
plt.subplot(1,2,1)
plt.psd(xs, Fs=1)
plt.subplot(1,2,2)
plt.psd(r_xs, Fs=1)
plt.subplots_adjust(wspace=0.5)
plt.show()

f:id:richard392742:20180918050025p:plain

右がロジスティックマップ,左が一様乱数によるPSD. PSDを見ても明確な違いを見出すことは難しい.

さらにAR(p)モデルの係数を見てみる.

from statsmodels.tsa.ar_model import AR

ar1 = AR(xs).fit(ic='aic')
ar2 = AR(r_xs).fit(ic='aic')

print('AR coefficients of logistic map:', ar1.params)
print('AR coefficients of uniform:', ar2.params)

AR coefficients of logistic map: [0.49164474 0.01590249]
AR coefficients of uniform: [ 0.51560335 -0.04973176]

上がロジスティックマップ,下が一様乱数によるAR係数.AR係数でも両者の違いを見出すのは難しい.

リターンマップによる可視化

1次元時系列$x(t)$を2次元状態空間$(x(t),x(t+1))$にプロットした図をリターンマップといい,カオス時系列にはしばしば用いられる.
先程の時系列をリターンマップで見てみる.

plt.figure(figsize=(10,4))
plt.subplot(1,2,1)
plt.scatter(xs[:-1],xs[1:],s=1)
plt.xlabel('x(t)')
plt.ylabel('x(t+1)')
plt.subplot(1,2,2)
plt.scatter(r_xs[:-1],r_xs[1:],s=1)
plt.xlabel('x(t)')
plt.ylabel('x(t+1)')
plt.subplots_adjust(wspace=0.5)
plt.show()

f:id:richard392742:20180918050029p:plain

右がロジスティックマップ,左が一様乱数によるリターンマップ. 両者の違いは一目瞭然である.
このようにカオス時系列解析での手法を使用すると,線形理論に基づく解析でわからなかった特徴を抽出することができる.

リターンマップはシステムによる$x(t)$から$x(t+1)$への写像を図示している.
例えば右のリターンマップの時系列を生成しているロジスティックマップの方程式は$x(t+1)=-4{x(t)}^2+4x(t)$であったが,この関係はリターンマップに良く表れている.

決定論的カオスの特徴

  1. 軌道不安定性：初期値に与えた変位が指数的に拡大する性質.つまり,初期値として与えた2点が時間経過とともに指数的に離れていく.この差の拡大率はリアプノフ指数という指標で定量化される.
  2. 長期予測不安定性：1.の性質から,無限大の精度で初期状態を観測しない限り,観測誤差は指数的に増大してしまう.ゆえに長期的な予測は実現不可能である性質.
  3. 有界性：非線形効果により,有界な領域に解が常に存在する性質.1.で変位は指数的に増大するものの,発散はしない.力学系の（十分時間が経過した）解軌道の集合のことをアトラクタという.
  4. アトラクタのフラクタル性,自己相似性：カオス力学系のアトラクタの幾何学的な構造は多くの場合自己相似性（フラクタル構造）をもつ.自己相似性はフラクタル次元と呼ばれる非整数の指標で定量化される.
  5. 非周期性

カオスが存在する実データ

  • 神経応答,脳波信号：「合原 一幸. "ニューラルシステムにおけるカオス". 東京電機大学出版局, March 1993」,「池口 徹，合原一幸，伊東 晋，宇都宮敏男. "カオスニューラルネットワークの次元解析", 電子情報通信学会論文誌 A, Vol.J73-A, No. 3, pp. 486-494 (1990).」,「池口 徹. "脳波とカオス" 数理科学, No.381 (1995年3月号), pp.36-43, サイエンス社 (1995年2月).」,「IKEGUCHI, Tohru, et al. "An analysis on Lyapunov spectrum of electroencephalographic (EEG) potentials." IEICE TRANSACTIONS (1976-1990) 73.6 (1990): 842-847.」
  • 心電図：「Richter, Marcus, and Thomas Schreiber. "Phase space embedding of electrocardiograms." Physical Review E 58.5 (1998): 6392.」
  • 工学システム：「合原 一幸. "カオス―カオス理論の基礎と応用". サイエンス社, September 1990.」,「合原 一幸（編）. "応用カオス―カオスそして複雑系へ挑む". サイエンス社, June 1994.」
  • 経済活動：「寺崎健, et al. "経済時系列データの決定論的非線形ダイナミカル特性に関する解析." 電子情報通信学会論文誌 A 78.12 (1995): 1601-1617.」
  • 音声信号：「Mende, Werner, Hanspeter Herzel, and Kathleen Wermke. "Bifurcations and chaos in newborn infant cries." Physics Letters A 145.8-9 (1990): 418-424.」,「Herzel, Hanspeter. "Bifurcations and chaos in voice signals." Applied Mechanics Reviews 46.7 (1993): 399-413.」,「Narayanan, Shrikanth S., and Abeer A. Alwan. "A nonlinear dynamical systems analysis of fricative consonants." The Journal of the Acoustical Society of America 97.4 (1995): 2511-2524.」,「Tokuda, Isao, Ryuji Tokunaga, and Kazuyuki Aihara. "A simple geometrical structure underlying speech signals of the Japanese vowel/a." International Journal of Bifurcation and Chaos 6.01 (1996): 149-160.」,「Kumar, Arun, and S. K. Mullick. "Nonlinear dynamical analysis of speech." The Journal of the Acoustical Society of America 100.1 (1996): 615-629.」

参考書籍

合原一幸(編). "カオス時系列解析の基礎と応用" 産業図書(2000).