はじめに

力学系のアトラクタを得ることはカオス時系列解析を行うためには非常に重要です.
しかし現実問題として力学系の時系列 ${\boldsymbol{x}(t)}$ そのものが得られることはまれで, 大抵は力学系を観測することによって得られた1次元の観測時系列 $\{y_n\}$ しか得られません.

${\boldsymbol{x}(t)}$ と ${y_n}$ の関係は以下のようにして数式で表されます.

${\begin{align} y_n = g(\boldsymbol{x}(n\Delta t)) + \eta_n \end{align}}$

だたし, 関数 $g$ は観測操作に相当する関数, $\Delta t$ はサンプリング間隔, $\eta_n$ は観測ノイズ.
我々が得ている時系列は大抵 ${y_n}$ と同様のプロセスを踏んでいます. ${y_n}$ から元の力学系のアトラクタを再構成するためにはどうすれば良いのでしょうか？

この話をローレンツ方程式を例にして具体的に考えてみます. ローレンツ方程式は以下で表される力学系です.

${\displaystyle \begin{align} \frac{dx}{dt}&=-px+py\\ \frac{dy}{dt}&=-xz+rx-y\\ \frac{dz}{dt}&=xy-bz \end{align}}$

ローレンツ方程式は3次元の力学系で下のような軌跡を描きます（アトラクタ）.

f:id:richard392742:20180923200155p:plain — ローレンツ方程式の状態変数の軌跡（アトラクタ）

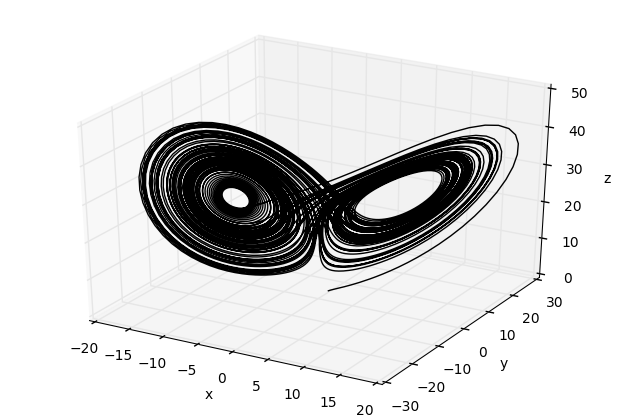
実際に時系列解析が行われるときは, この力学系 $x,y,z$ 全ての時系列が得られることはまれで, 観測により $x$ のみの時系列が得られるようなケースが多いです（つまり観測時系列は $g(\boldsymbol{x})=x, \eta_n=0$ で得られた）.

f:id:richard392742:20181008025736p:plain — ローレンツ方程式のxの時系列

このようなとき, $x$ の時系列のみで元の3次元の力学系の構造や振る舞いを把握することは可能でしょうか？

時間遅れ座標系とTakensの埋め込み定理

アトラクタの再構成のために良く使用されるのが「時間遅れ座標系」と呼ばれる座標系への変換です. この変換では観測時系列 $\{y_n\}$ は以下の様に $m$ 次元ベクトルの時系列 $\{\boldsymbol{v}_n\}$ 変換されます.

${\displaystyle \begin{align} \boldsymbol{v}_n = (y_n,y_{n-\tau},\dots,y_{n-(m-1)\tau}) \end{align}}$

ただし, $\tau$ は時間遅れの大きさ. また $\boldsymbol{v}$ の次元数 $m$ は埋め込み次元と呼ばれます.

このようにして構成された遅れ座標系は本当に元の力学系のアトラクタを再構成できるのでしょうか？また, 再構成ができるのであれば $m$ はいくつにすればいいのでしょうか？これらの問題は「Takensの埋め込み定理」により保証されています.

Takensの埋め込み定理

$d$ 次元のコンパクトな多様体 $D$ と $C^1$ 級写像 $\boldsymbol{f}:D\to D, g:D\to \mathbb{R}^1$ が与えられたとき, $m>2d$ であれば, 次式の写像 $V:D\to \mathbb{R}^m$ は埋め込みである.

${\begin{align} V(\boldsymbol{x})=(g(\boldsymbol{x}),g(\boldsymbol{f}(\boldsymbol{x})),g(\boldsymbol{f}^2(\boldsymbol{x})),\dots,g(\boldsymbol{f}^{m-1}(\boldsymbol{x}))) \end{align}}$

「埋め込み」について

「埋め込みである」とはどういう意味でしょうか？
ある多様体 $D$ に対し, 写像 $V$ が埋め込みであるとは, 写像 $V$ が以下を満たすということです.

$V$ が1対1写像である
$V$ の微分が1対1写像である
$D$ に対し, $V$ が同相写像(位相空間 $A,B$ の間の写像 $f:A→B$ が連続かつ全単射で, その逆写像もまた連続である写像のこと)である

1.と2.の性質について下図の例で見てみます.

f:id:richard392742:20181006023011p:plain

この図では多様体 $M$ が写像 $V$ により写されたときを3つのパターンで示しています.

$V$ が埋め込みのときは一番右のようになります.
$V$ が2.の性質を満たしていない場合は真ん中のように微分が不可能な部分ができます.
$V$ が1.の性質を満たしていない場合は左のように重なって1対1とならない部分ができます.

このように $\boldsymbol{x}$ の軌道が再構成されるためには図の真ん中や右のようにはならず, かつ同相である写像でなければなりません.
Takensの埋め込み定理の「埋め込みである写像」とは「元の力学系の構造や振る舞いを保存する写像」と解釈できます.

写像 $V$ について

Takensの埋め込み定理の写像 $V$ は「力学系を観測し, 観測時系列を遅れ座標系にする」という操作に対応しています.
$V$ 内の関数 $\boldsymbol{f}$ を力学系の状態変数 $\boldsymbol{x}$ を一時刻先へ時間発展をさせる関数 $\boldsymbol{f}:\boldsymbol{x}_t \to \boldsymbol{x}_{t+1}$ と考えます. そうすれば

${\begin{align} \boldsymbol{x}_t,\boldsymbol{f}(\boldsymbol{x}_t),\boldsymbol{f}^2(\boldsymbol{x}_t),\dots,\boldsymbol{f}^{m-1}(\boldsymbol{x}_t)=\boldsymbol{x}_t,\boldsymbol{x}_{t+1},\dots,\boldsymbol{x}_{t+m-1} \end{align}}$

となります.
これに観測関数 $\boldsymbol{g}$ をかけると観測時系列になり, さらに, これは写像 $V$ でもあります.

${\begin{align} (y_t,y_{t+1},\dots,y_{t+(m-1)}) &=\boldsymbol{g}(\boldsymbol{x}_t,\boldsymbol{x}_{t+1},\dots,\boldsymbol{x}_{t+m-1})\\ &=(g(\boldsymbol{x}_t),g(\boldsymbol{f}(\boldsymbol{x}_t)),g(\boldsymbol{f}^2(\boldsymbol{x}_t)),\dots,g(\boldsymbol{f}^{m-1}(\boldsymbol{x}_t)))\\ &=V(\boldsymbol{x}_t) \end{align}}$

今回 $\boldsymbol{f}$ は時間発展の関数としていましたが, 逆に時間を遅れさせる関数 $\boldsymbol{f}:\boldsymbol{x}_{t+1} \to \boldsymbol{x}_t$ としても良く, そうすると上の観測時系列は遅れ座標系になります.
また, 一時刻を $\tau$ とすれば $(y_n,y_{n-1},\dots,y_{n-(m-1)}) \to (y_n,y_{n-\tau},\dots,y_{n-(m-1)\tau})$ ではじめの遅れ座標系と同じになります.

Takensの埋め込み定理が言いたいこと

Takensの埋め込み定理は遅れ座標系を導入したとき, 元の力学系の構造や振る舞いが保存されるのに十分な $m$ の値を与えてくれています. 元の力学系の次元数 $d$ に対し, $m=2d+1$ 以上とすれば十分であることを保証しています.
なぜ元の次元数の2倍より大きな $m$ が必要なのでしょうか？
ここで下図のような $\mathbb{R}^d$ 上の1次元多様体 $D$ を様々な $m$ での写像 $V$ で写すことを考えてみます.

f:id:richard392742:20181006023042p:plain

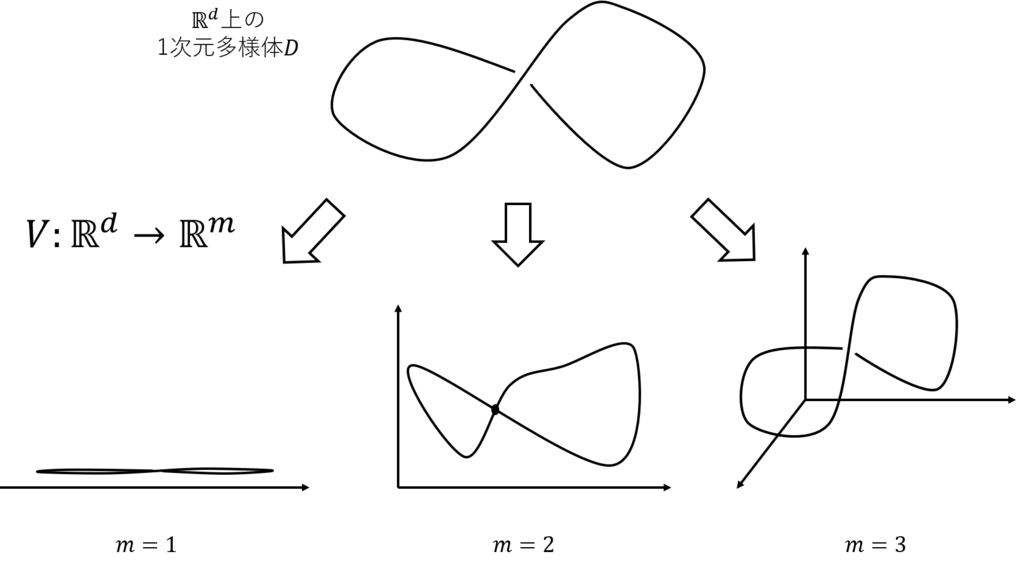
$m=1$ のときは元の多様体上の点が重なり軌道が再構成できないことがわかります.
$m=2$ のときも重なる部分があり, 軌道を完全には再構成できません.
$m=3$ のときは重なるようなことはほぼありません. 例え重なるようなときでも観測関数に摂動を加える（現実ではこれは観測ノイズとして必ず入ってくる）ことで重なりは容易に解消されます.

実際にやってみる

先のローレンツ方程式で確認してみましょう.

import numpy as np
from scipy.integrate import ode
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 力学系のパラメータ設定
p = 10.0
r = 28.0
b = 8.0/3.0

# 力学系の関数を設定
def x_dot(x, y):
    return -p*x + p*y

def y_dot(x, y, z):
    return - x * z + r * x - y

def z_dot(x, y, z):
    return x * y - b * z

def lorenz(t, v):
    '''v = [x, y, z]'''
    return [x_dot(v[0],v[1]), y_dot(v[0],v[1],v[2]), z_dot(v[0],v[1],v[2])]

# 初期値の設定
t0 = 0.0
x0, y0, z0 = 1.0, 1.0, 1.0

# シミュレーションの時間間隔
dt = 0.01

# シミュレーション時間
T = 100.0

# 数値計算を行うオブジェクトの作成
integrator = ode(lorenz).set_integrator('dopri5')
integrator.set_initial_value([x0,y0,z0], t0)

# シミュレーション
time = []
data = []
for t in np.arange(t0, T, dt):
    time.append(integrator.t+dt)
    data.append(integrator.integrate(integrator.t+dt))
data = np.array(data)

# 観測によりxの時系列を得る
x = data[:, 0]

# アトラクタ再構成
def get_delay_coordinate(x, dt, m, tau):
    interval = tau/dt
    vs = [np.array([x[i-int(interval*j)] for j in range(m)])
         for i in range(int(interval*(m-1)), len(x))]
    return vs

tau = 0.1
m = 3

vs = get_delay_coordinate(x, dt, m, tau)
vs = np.array(vs)

fig = plt.figure()
ax = Axes3D(fig)
ax.plot(vs[:,0], vs[:,1], vs[:,2], lw=1, c='k')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()

f:id:richard392742:20181008055902p:plain — $m=3, \tau=0.01$ のとき

f:id:richard392742:20181008055824p:plain — $m=3, \tau=0.01$ のとき

f:id:richard392742:20181008055829p:plain — $m=3, \tau=0.1$ のとき

f:id:richard392742:20181008055832p:plain — $m=3, \tau=0.1$ のとき

f:id:richard392742:20181008055847p:plain — $m=3, \tau=1.0$ のとき

f:id:richard392742:20181008055858p:plain — $m=3, \tau=1.0$ のとき

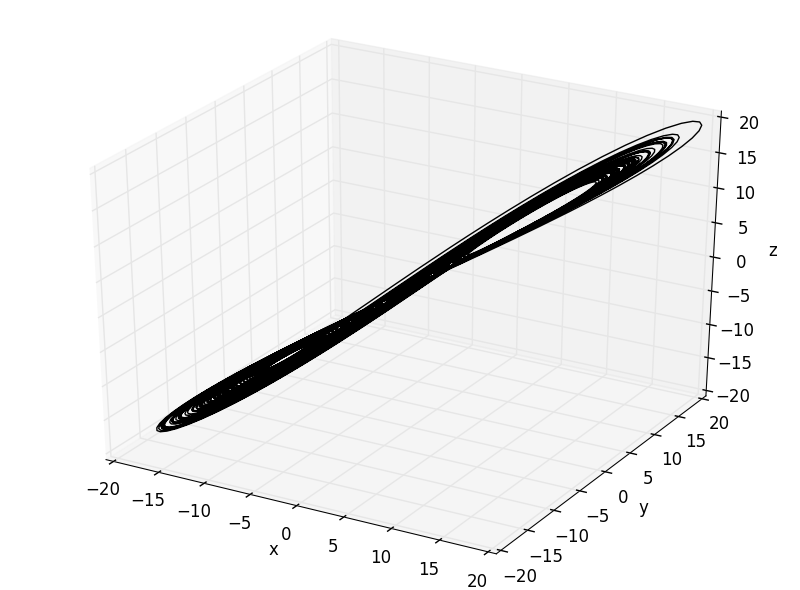
f:id:richard392742:20181008063728p:plain:w200 — $m=2, \tau=0.1$ のとき

この中では $m=3, \tau=0.1$ のとき, 最も上手くいっており, 1次元の遅れ座標系の軌跡が元のアトラクタとよく似ているように見えます.
本来であればローレンツ方程式は3次元力学系なのでTakensの埋め込み定理が保証してくれるのは $m=7$ からですが, Takensの埋め込み定理は十分条件なのでこのように実は $m=3$ でも元のアトラクタが再構成できてしまうこともあります. $m$ の最小値を求めるには, 「False nearest neighbors」などの手法を使用する必要があります(~~今までのは何だったのか~~).
また, Takensの埋め込み定理では $\tau$ はほぼ任意であるのですが, 現実的にはデータの有限性やノイズなどの理由から, やはり $\tau$ も最適なものを求める必要があります. 方法としては自己相関関数を使用して求めるようです.

参考

合原一幸(編). "カオス時系列解析の基礎と応用" 産業図書(2000). Kantz, Holger, and Thomas Schreiber. Nonlinear time series analysis. Vol. 7. Cambridge university press, 2004. Hegger, Rainer, Holger Kantz, and Thomas Schreiber. "Practical implementation of nonlinear time series methods: The TISEAN package." Chaos: An Interdisciplinary Journal of Nonlinear Science 9.2 (1999): 413-435.

りちゃｒｄ blog

カオス時系列解析 -観測時系列からのアトラクタ再構成-

はじめに

時間遅れ座標系とTakensの埋め込み定理

Takensの埋め込み定理

「埋め込み」について

写像 $V$ について

Takensの埋め込み定理が言いたいこと

実際にやってみる

参考

はじめに

時間遅れ座標系とTakensの埋め込み定理

Takensの埋め込み定理

「埋め込み」について

写像について

Takensの埋め込み定理が言いたいこと

実際にやってみる

参考

写像 $V$ について