カオス時系列解析 - 力学系とアトラクタ -
力学系とは?
力学系とはある時刻における状態が、微分方程式、差分方程式、微差分方程式により決定されるシステムのこと。
$k$次元力学系では、任意の時刻におけるシステムの状態の変化則は$k$個の状態変数の関数により記述される。
離散時間力学系の場合: $$ x(t+1)=\boldsymbol{f}_\boldsymbol{\mu}(\boldsymbol{x}(t)) $$
連続時間力学系の場合: $$ \frac{dx(t)}{dt}=\boldsymbol{f}_\boldsymbol{\mu}(\boldsymbol{x}(t)) $$
但し、$\boldsymbol{x}(t)$は時間$t$における力学系の状態空間を構成する多様体上のシステムの状態、$\boldsymbol{f}$は$k$次元の非線形関数、$\boldsymbol{\mu}$はシステムを制御するパラメータベクトル。
先述のこれらの式のように$\boldsymbol{f}$内に明示的に時間$t$が含まれていない系を自律系(automonous system)という。これに対し、
$$ x(t+1)=\boldsymbol{f}_\boldsymbol{\mu}(\boldsymbol{x}(t),t) $$
や $$ \frac{dx(t)}{dt}=\boldsymbol{f}_\boldsymbol{\mu}(\boldsymbol{x}(t),t) $$
のように$\boldsymbol{f}$内に明示的に時間$t$が含まれている系を非自律系(non-automonous system)という。
アトラクタとは?
力学系に初期条件を与え、十分時間が経った後の$k$次元状態空間内での漸近的な振る舞いのこと。
例として以下で与えられるローレンツ方程式のアトラクタを見てみる。
ローレンツ方程式:
$$
\begin{eqnarray}
\frac{dx}{dt}&=&-px+py\\
\frac{dy}{dt}&=&-xz+rx-y\\
\frac{dz}{dt}&=&xy-bz
\end{eqnarray}
$$
但し、$p,r,b$はそれぞれシステムを制御するパラメータで、$p=10,r=28,b=\frac{8}{3}$のとき、ローレンツ方程式はカオス的な挙動をすることが知られている。
参考:https://ja.wikipedia.org/wiki/%E3%83%AD%E3%83%BC%E3%83%AC%E3%83%B3%E3%83%84%E6%96%B9%E7%A8%8B%E5%BC%8F
import numpy as np from scipy.integrate import ode import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D # 力学系のパラメータ設定 p = 10.0 r = 28.0 b = 8.0/3.0 # 力学系の関数を設定 def x_dot(x, y): return -p*x + p*y def y_dot(x, y, z): return - x * z + r * x - y def z_dot(x, y, z): return x * y - b * z def lorenz(t, v): '''v = [x, y, z]''' return [x_dot(v[0],v[1]), y_dot(v[0],v[1],v[2]), z_dot(v[0],v[1],v[2])] # 初期値の設定 t0 = 0.0 x0, y0, z0 = 1.0, 1.0, 1.0 # シミュレーションの時間間隔 dt = 0.01 # シミュレーション時間 T = 100.0 # 数値計算を行うインスタンスの作成 integrator = ode(lorenz).set_integrator('dopri5') integrator.set_initial_value([x0,y0,z0], t0) # シミュレーション time = [] data = [] for t in np.arange(t0, T, dt): time.append(integrator.t+dt) data.append(integrator.integrate(integrator.t+dt)) data = np.array(data) # 描画 fig = plt.figure() ax = Axes3D(fig) ax.plot(data[:,0], data[:,1], data[:,2], lw=1, c='k') ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') plt.show()
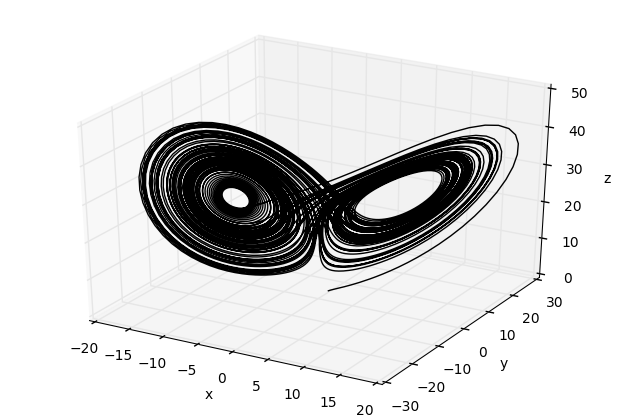
アトラクタの種類
アトラクタの形状は以下のように分類される。
1. 平衡点
2. リミットサイクル
3. トーラス
4. ストレンジアトラクタ、カオス
参考
合原一幸(編). "カオス時系列解析の基礎と応用" 産業図書(2000).